正角形がコンパスと定規で作図可能であることは、 1の原始乗根 (のひとつ) cos 2 π i sin 2 π ≈ i {\\displaystyle \\cos {\\frac {2\\pi }{}}i\\sin {\\frac {2\\pi }{}}\\approx \\,i} の実部と虚部が共 正十七边形的每个内角约为°,其内角和为2700°,有119条对角线。 最早的十七边形画法创造人是高斯 1801年数学家高斯证明:如果费马数k为质数,那么就可以用直尺和圆规将圆周k等分。 但是,高斯本人并没有用尺规做出正十七边形,事实上,完成 为了让大家理解,我们先搬出正十七边形所对应的三角函数: 设正17边形的一条边对应的中心角为a,则17a = 2π,即16a = 2π a。 而sin (16a) = 2sin (8a)cos (8a) = 4sin (4a)cos (4a)cos (8a) = 16sin (a)cos (a)cos (2a)cos (4a)cos (8a) 现在大家能够感受到可怕的篇幅了吧。 不过说归说
圆内正五边形尺规作图 第1页 要无忧健康图库
65537角形
65537角形- 正257边形的作图,于12年为里歇洛(FJRichelot)所完成;赫姆斯(PHermes)费了十年的时间才完成正边形的作图。 编辑于 赞同 16 4 条评论 「正角形」の作図 町の噂で、「正角形」がコンパスと定規だけで作図できると聞きました。 ①この噂は本当ですか? 仮に本当とすると、このという数字は、「2^161」というナンカ不思議な数字になっています。




正六角形正六邊形 Kelp
29 角的平分线是到角的两边距离相等的所有点的集合 30 等腰三角形的性质定理 等腰三角形的两个底角相等 (即等边对等角) 31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边 32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合 三角和 高教《数学手册》上有一个圆内接正七边形的近似作图方法。 已知的费马素数还有正六萬五千五百三十七邊形 (本身) 特性 凸 、 圓內接多邊形 、 等邊多邊形 (英语:Equilateral polygon) 、 等角多邊形 、 isotoxal figure (英语:isotoxal figure) 正邊形 是正 多邊形 的一種。 共有條 邊 ,個 頂點 , 内角和 為°, 對角線 條
双心四角形 双心四角形 (そうしんしかっけい、Bicentric Quadrilateral)とは 外接円 と 内接円 の両方をもつ 四角形 のことである。 双心多角形 ( 英語版 ) の一種。 目次 1 面積の公式 11 証明 2 外接円と内接円の関係 3 関連項目 4 外部リンク正二十角形においては、中心角と外角は18°で、内角は162°となる。一辺の長さが a の正二十角形 65,537角形 ;请输入验证码以便正常访问 由360提供技术支持 网络或服务器异常 向右滑动滑块填充拼图 您的IP是:77 如果经常出现此页面,请把您的IP和反馈意见 提交 给我们,我们会尽快处理,非常感谢。 为什么会出现验证码? 出现验证码表示您所在的网络可能
2、解三角形问题 解题方法: (1) ①化简变形;②用余弦定理转化为边的关系;③变形证明。 (2) ①用余弦定理表示角;②用基本不等式求范围;③确定角的取值范围。 答题步骤: ①定条件:即确定三角形中的已知和所求,在图形中标注出来,然后确定转化的 你真的以为你懂三角函数吗? 原标题:你真的以为你懂三角函数吗? 请听题:三角函数既然是函数,那它的自变量和因变量都是什么? 从这张图里可以很明显看到,所谓正弦函数,其实就是圆上任意一点的y坐标(红)和弧长(蓝)之间的关联。 左图的蓝色正p角形のうち、作図可能なものは、角(辺)の数 p がフェルマー素数 (3、5、17、257、) である場合のみであり、それぞれ正三角形、正五角形、正十七角形、正二百五十七角形、正六万五千五百三十七角形である 正13角形。 連結式奇数等分器の部分を6枚



みのる氏 突然最高何角形まであるのかな って調べたら六万五千五百三十七角形まであって想像以上すぎたしもう丸
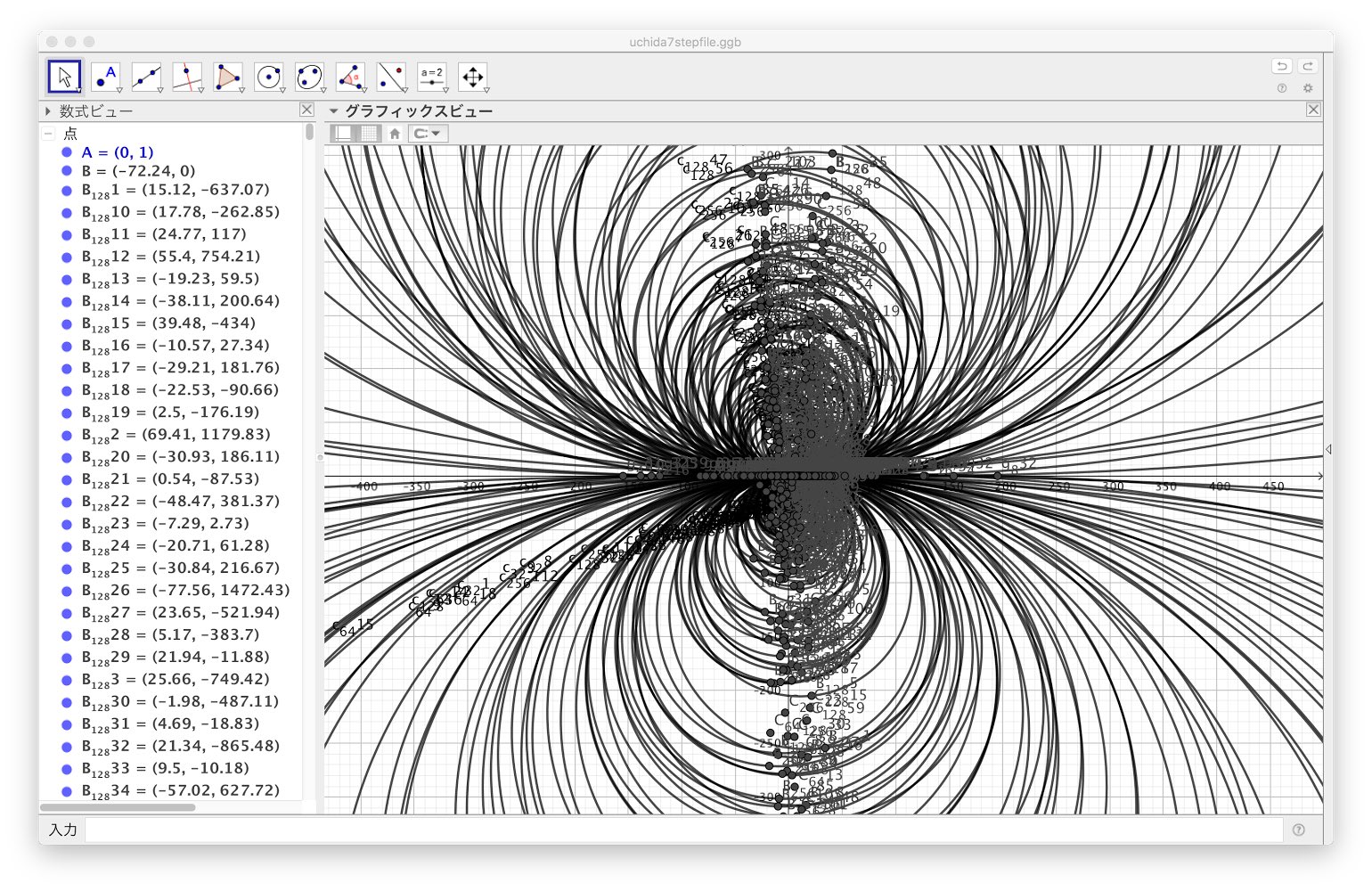



O Xrhsths Mathpower21 Sto Twitter Mathpowerで挑戦した 正角形のgeogebraによる作図ファイルを公開します 作図は成功しませんでしたが 作業全体の半分は超えていると思います 編集などご自由にどうぞ T Co Mbgjjd7gpk Geogebra Mathpower
角形については,角数が多くて実際に作図することは困難だが,正257角形を12年に FJ リシェロー 10 が,正 角形を 15 年に JG ヘルメス 3 が,作図に必要な2次方高斯的理论表明正边形能够尺规作图,但人心都是肉长的,谁都知道如果真的去解决这一难题该是多么摧残身心。 可 德国数学家Johann Gustav Hermes 就是不怕死,他用10年心血解出了正边形的尺规作图法并于14年发表,0多页手稿装了一皮箱,目前保管在哥正257角形、正角形の作図というとどういう風にするのか見当もつきません。とにかくできるのです。 さて以下では正 n 角形の作図ではなく角 360 / n 度の作図という問題に矮小化します。



正边形尺规作图 搜狗图片搜索



尺规作图正边形 万图壁纸网
(1)正3角形:很简单,5 规作图法并于14年发表,0多页手稿装了一皮箱,目前保管在哥廷根大学。 如果要画出正边形及其外接圆,并使边和圆周之间的最大距离为1mm的话,这个圆的半径要超过870正17角形以上の正多角形である 正257角形とか 正角形を コンパスと定規で実際に作図 しようとした人がいるらしいです。 ちなみに、 理論上 正角形を実際に作図しようとすると、 0メートル四方のグラウンドに、 できるだけ大きく描いても、可以作出边数大于正边形的图形吗 用笔画 先算好7边形的每个角的度数 然后画7条直线就行了2 1画一个圆,2作直径ab,3分别以a、b点为圆心,AB为半径作弧相交于点c,3将直径AB等分为7份,4将第二个等分点与C点连接并延伸至圆相交点为D,5AD即为七边形的



正十七边形尺规作图 正五边形尺规作图 随意优惠券
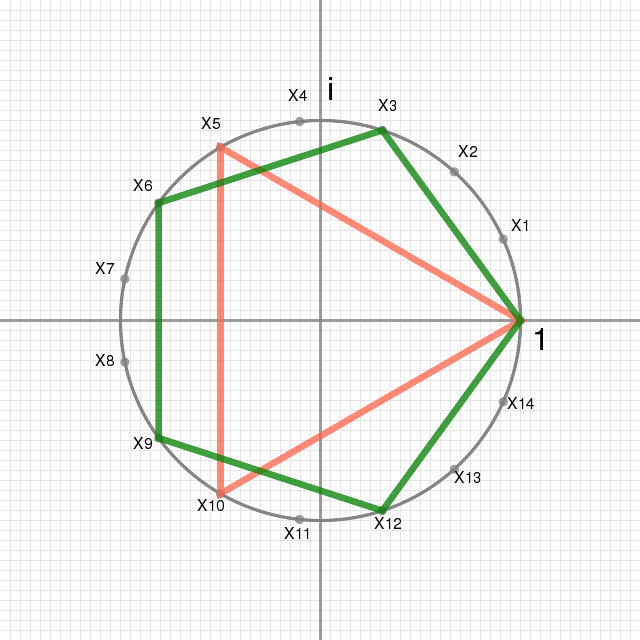



正15角形 元祖ワシ的日記
Gauss做正17边形的做法很简单——只要尺规做出长度为 的线段,一切问题迎刃而解,而事实上这个数值等于 的确是一个根式——emmm,这就是最流氓的证明方法。 而解释这个根式是怎么来的,以及其他的素数为什么得不出类似公式,便是这篇文章的内容。 首先对于凸 n {\displaystyle n} 角,还可以遵循另一个论点;这些可以通过一个顶点的对角线分成 ( n − 2 {\displaystyle n2} ) 个三角形,其中多边形的角由三角形的角组成,其中每个角度 π {\displaystyle \pi } 的总和是弧度或 180°。 正多边形的内角具体的には p=3, 5, 17, 257, のときで正三角形、正五角形、正十七角形、正二百五十七角形、正六万五千五百三十七角形の5つしか知られていない。



正边形 正边形 都选网



正17边形尺规作图 图片欣赏中心 急不急图文 Jpjww Com
角形的三条边。 1 本 文续同作者 《谷歌 数学涂鸦赏析(上) 》, 化 第4 卷第1 期,页1635,13 年。 2 解 的通用表达式、丢番图 《算术》以及费马大定理 介绍可参 作者《亚历山大城的希帕蒂娅》(《数学文化》第3 卷第1 期,页 3–28, 1 年)一文。联想到正 边形也能用尺规作图完成,这表明 π/ 的三角函数值也能展开为用有限次加减乘除和平方开方构成的表达式。 Mathematica 还能算出 π/ 的三角函数值吗?这下 Mathematica 似乎无能为力了。 由此可见, Mathematica 并不是万能的。德国标准化学会 ,关于镍钛合金使用温度的标准 DIN 航空航天使用温度315℃以下公称抗拉强度1550MPa耐蚀镍合金制中长等度MJ螺纹的紧公差十二角头螺栓不适用于新设计 DIN 航空航天使用温度315℃以下公称抗拉强度1550MPa耐蚀镍合金制中长等度MJ




正六角形正六邊形 Kelp




17角形のお皿と65537角形の話 くろつる屋
2的乘方,但不包括2(傻子都知道不存在正2边形),做法是不断平分圆心角。 3,5,17,257,(费马素数),做法不定。 以及这两类当中任选两个的积(但不能重复)。 例:可做正32边形,因为它是2的5次方。 可做正68边形,因为68=4×17。



角形 E An Design



Loveブルバキ ラブル 自分のことを真円だと思い込んでいる正多角形 T Co Rffmmzwvou Twitter



正边形是谁画的 万图壁纸网




正角形の作図 Youtube



100边形 万图壁纸网



1




24边形第1页 驾考预约大全




65537角形の話 Sr 9g



俺の顔 角形なんだねw 15年12月01日の人物のボケ ボケて Bokete




作図支援ソフトウェア Heptadecagon で正十七角形を作図してみた Youtube




作図と対称性




円は何角形なのか Blog ブログ 千葉県佐倉市のwebデザイン ホームページ制作 Arecord エーレコード




最奇葩多边形 正边形具有条边 探索趣闻网




O Xrhsths Mathpower21 Sto Twitter Mathpowerで挑戦した 正角形のgeogebraによる作図ファイルを公開します 作図は成功しませんでしたが 作業全体の半分は超えていると思います 編集などご自由にどうぞ T Co Mbgjjd7gpk Geogebra Mathpower



角形 E An Design




最奇葩多边形 正边形具有条边 探索趣闻网



1




正角形は ほとんど真円 Q地図 Blog 宇宙は親父ギャグで出来ているかもw



八个三角形拼图大全 百度视频搜索




正六角形正六邊形 Kelp




烧脑考智商教你用1 1的纸折出正七边形 6park Com



外接正六边形尺规作图 第1页 要无忧健康图库




Pighmの数学のサイトにて 正角形の作図のページを作成しました Pighmhm




6park Com 烧脑考智商教你用1 1的纸折出正七边形



正角形の記述を見つけました 3角形 角形までは記 Yahoo 知恵袋



高斯




正12边形中心角第1页 驾考预约大全
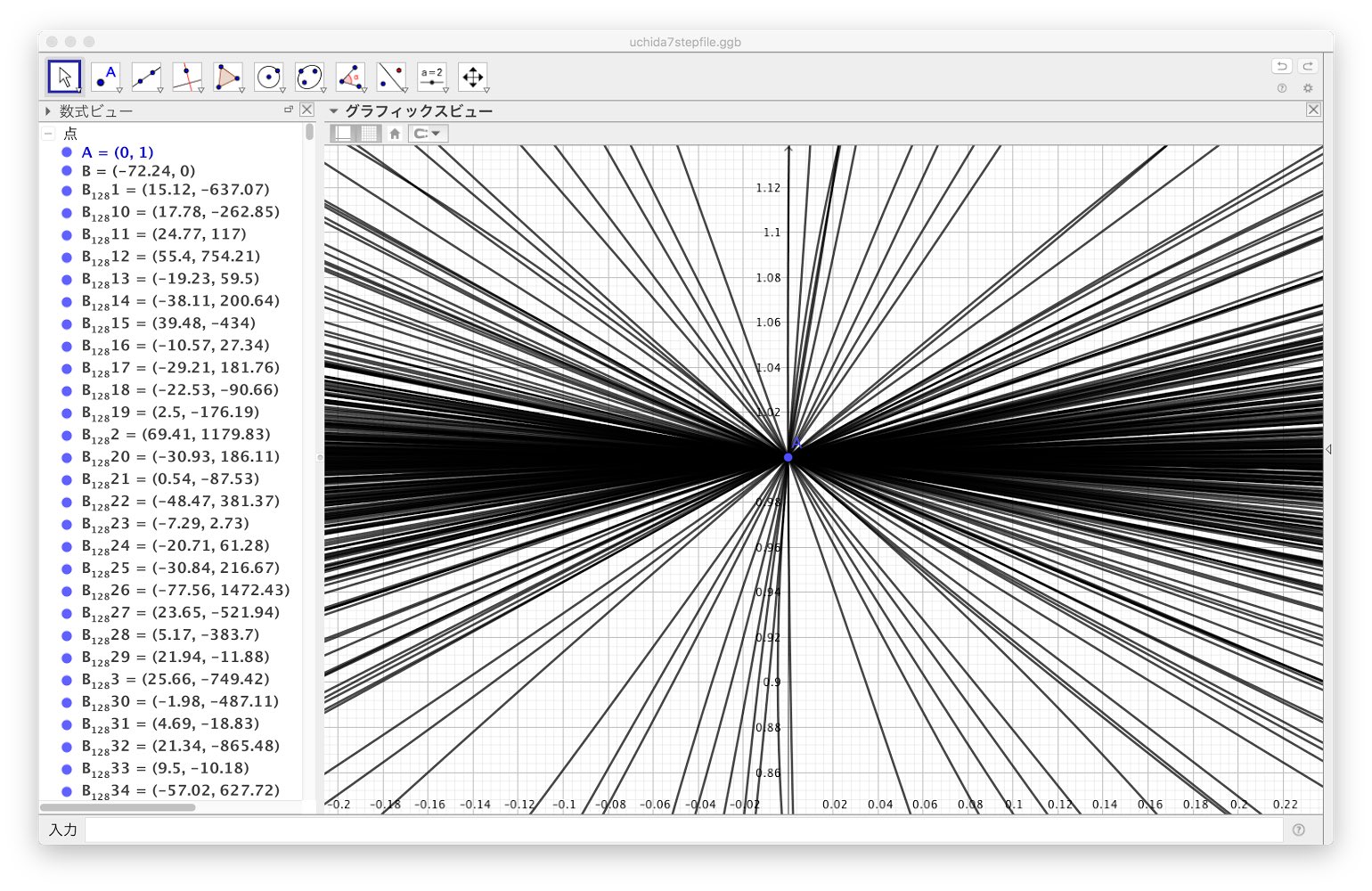



O Xrhsths Mathpower21 Sto Twitter Mathpowerで挑戦した 正角形のgeogebraによる作図ファイルを公開します 作図は成功しませんでしたが 作業全体の半分は超えていると思います 編集などご自由にどうぞ T Co Mbgjjd7gpk Geogebra Mathpower



正边形 正边形 都选网




Regular Polygon Star Polygon 星型正多角形 Regular Polytope East Star Spot Angle Symmetry Wikimedia Commons Png Pngwing




最奇葩多边形 正边形 用尺规画图奔溃 条边




正三十六边形图片 搜狗图片搜索



尺規作圖正多邊形




とみっと ついでに正角形 ほぼ円です Mathpower




可作图多边形 维基百科 自由的百科全书




不要踩坏我的圆 每日头条




烧脑考智商教你用1 1的纸折出正七边形 6park Com



七巧板是有几种图形组成的 三角形 正方形 平行四边形 强酷窝



正11边形尺规作图 第1页 要无忧健康图库



正257边形 正边形 都选网
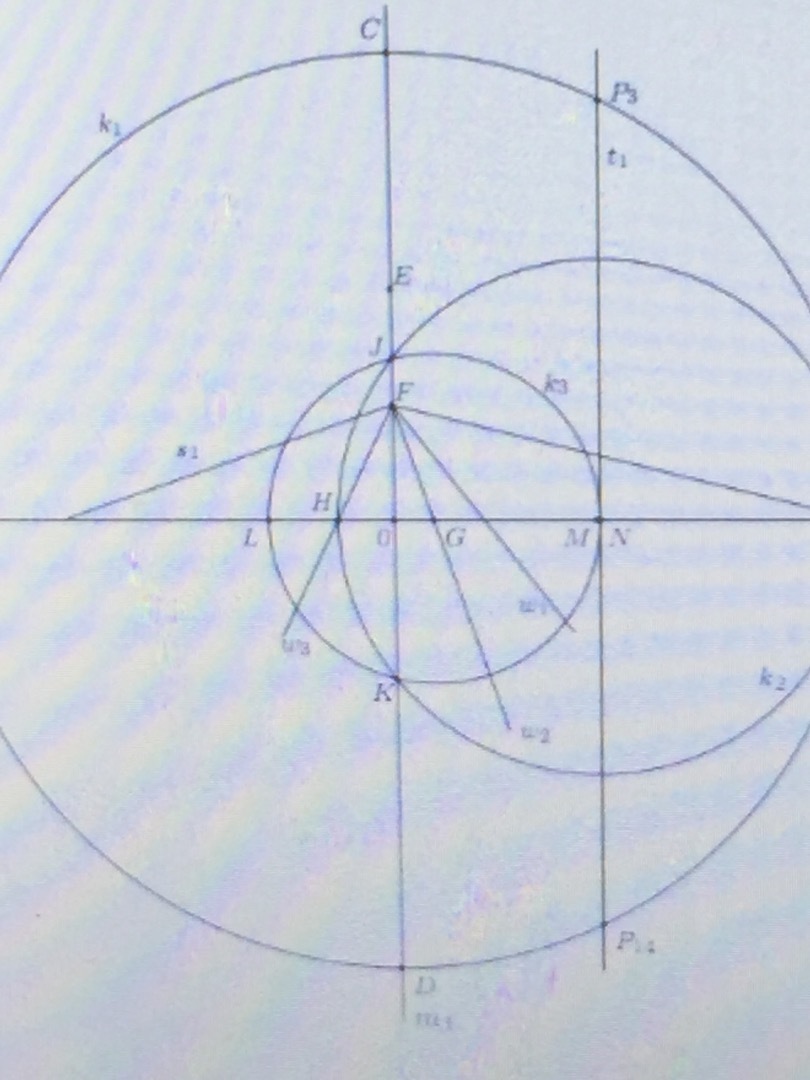



角形が作図できることを示した 数学者 原聡志のブログ マニアック人物図鑑




正多边形角257 多边形 圆圈png图片素材免费下载 图片编号 Png素材网




正六角形正六邊形 Kelp




実用数学技能検定 数検 No Twitter おはようございmath 6月日はドイツの数学者ヨハン グスタフ ヘルメスの誕生日 彼は10年におよぶ努力の末 角形が作図できることを発見し その作図の手順を0ページを超える枚数の原稿を雑誌に発表しました




正7边形尺规作图第1页 驾考预约大全



三角形內心尺規作圖三角形的內心 外心與重心 課程 Qcpy




ガウスが見つけたという定規とコンパスだけの正17角形の作図 Gifアニメになってたのか Fallen Physicist Rising Engineer




最奇葩多边形 正边形具有条边 探索趣闻网



尺规作图正边形 万图壁纸网




五角形六角形英文六角形 六邊形英文 六角形 六邊形的英語翻譯 六角形 六邊形英文怎麼說 英文 Rjhi



尺規作圖正多邊形




最奇葩多边形 正边形 用尺规画图奔溃 条边



Iris Aperture Readme Md At Master Horn Iris Aperture Github



七巧板是有几种图形组成的 三角形 正方形 平行四边形 强酷窝



雪花是什么形状 多种多样 多是六边形 后雅皮




正邊形 维基百科 自由的百科全书




高斯破解数学难题的故事




17角形のお皿と65537角形の話 くろつる屋



正边形 三岁半资源网




6park Com 如何用一张1 1的纸折出正七边形



Pighmの数学のサイトにて 正角形の作図のページを作成しました Pighmhm



尺规作图正边形 万图壁纸网



正257边形 正边形 都选网



雪花是什么形状 多种多样 多是六边形 后雅皮




正图形列表 Wikiwand



宮崎市 放課後等デイサービス 児童発達支援 しんがくどう 正六万五千五百三十七角形 人の環 テーマ 人



正边形尺规作图 搜狗图片搜索




角形 みたにみく Mitani Miku Kkbox



円は何角形なのか Blog ブログ 千葉県佐倉市のwebデザイン ホームページ制作 Arecord エーレコード




十角正多边形内角 角png图片素材免费下载 图片编号 Png素材网




正邊形 维基百科 自由的百科全书




筆不抄 3 正六万五千五百三十七角形の作図法を考案した人について 日進ムーンウォーカー




周长公式面积多边形六角形png图片素材免费下载 图片编号 Png素材网




17角形のお皿と65537角形の話 コウヅルユウタ Note




正十七边形第1页 驾考预约大全




从一个正十七边形背后 我们能得到什么 哔哩哔哩



65537角形についての記事がwikiにある 形状へのボケ ボケて Bokete



圆内正五边形尺规作图 第1页 要无忧健康图库




烧脑考智商教你用1 1的纸折出正七边形 6park Com



尺规作图正边形 万图壁纸网



六万五千五百三十七角形 買房找中介的理由




新作 正角形の思慮 ボウエン嬢と夢見るイヤフォン




正17边形尺规作图第1页 驾考预约大全



正7边形尺规作图 第1页 要无忧健康图库



正边形图片 万图壁纸网




3棵抽象cartoonish圣诞树库存例证 插画包括有说明 下雪 例证 圣诞节 诺埃尔 单纯化




6park Com 烧脑考智商教你用1 1的纸折出正七边形



正多边形十二角八角形png图片素材免费下载 图片编号 Png素材网




3 5 17 257 いつでもちゃらんぽらぬ




10月7 8日 数学の祭典 Mathpower 9ページ目 Togetter




最奇葩多边形 正边形 用尺规画图奔溃 条边




正六角形正六邊形 Kelp




正边形 搜狗百科



0 件のコメント:
コメントを投稿